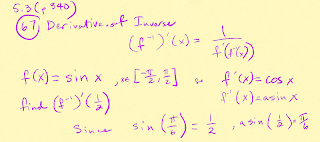More Definite Integrals and the Area Under a Curve (4.4 p 293 # 62)
Thursday, December 2, 2021
More definite Integrals and Area under a Curve (4.4 p 293 # 62)
Friday, November 26, 2021
MVT for Integrals, 1st FTC, and 2nd FTC Proofs
Section 4.4 is chock full of gold. There is a lot there, so the video lets you take it in.
Here are the Subjects by Time:
0:00 - The MVT for integrals (Average Value Thm) & AVERAGE VALUEs
4:20 - An example with f(x) =6 and a curious observation
6:24 -The First Fundamental Theorem Proof
11:16 - An Example of FTC1
12:51 - "Net Change Theorem" version of FTC1 with a "word problem" example
15:27 -The Second Fundamental Theorem of Calculus with for examples
19:05 - The End
Sunday, October 17, 2021
Wednesday, February 3, 2021
Monday, February 1, 2021
Elliptical Orbit in a Polar Form (10.6 p745 #59)
If you want to skip ahead:
Minute 5:45 Finding the distance between the surface of Earth and Explorer 18 when the angle is 60 degrees
Minute 12:53 Proof that e = c/a = 2c/2a=(distance between focii/major axis)
Sunday, January 31, 2021
A Bounded Area (def Int) with log base 4 (5.5 p359 #81)
A Bounded Area (def Int) with log base 4 (5.5 p359 #81)
This one has u substitution a a conversion from base 4 to bas e, confirming with the TI-84
An Indefinite Integral with Exponents (5.5 p 359 #76)
An Indefinite Integral with Exponents (5.5 p 359 #76)
This includes u-substitution, and an exponential function in base 2
Proving an old Compounded Interest Formula with L'Hôpital's Rule (5.6 p371 #90)
We demonstrate the ln technique as well as makeing a product into a ratio so you can use L'Hôpital's Rule.
Implicit Diff with arctan (5.7 p 380 #71)
Implicit Diff with arctan (5.7 p 380 #71)
Here we find a tangent line of a function using implicit differentiation, the product rule, the chain rule, and some careful algebra.
The Derivative of an Inverse Function (5.3 p340 #67)
The Derivative of an Inverse Function (5.3 p340 #67)
The derivative of a inverse function is the reciprocal of the derivative of the inverse function. Be mindful of the exchange of values (x,y) to (y,x) with inverse functions
Sunday, January 24, 2021
Inverse Functions (5.3 p 340 #53)
Inverse Functions (5.3 p 340 #53)
We have more than just the horizontal line test now, if a function is strictly monotonic, it will have an inverse.
Saturday, January 23, 2021
Wednesday, January 20, 2021
Slope Fields and Differential Equations with Natural Logs (5-2 p330 #49)
Slope Fields and Differential Equations with Natural Logs (5-2 p330 #49)
A slope field and a diffyQ checked with the TI-84
Tuesday, January 19, 2021
Long Division Before Integrating (5-2 p330 #17)
Long Division Before Integrating (5-2 p330 #17)
This one looks like a difficult u-sub, but turns out to be easy after long division!
Monday, January 11, 2021
A Tangent Line Confirmed with the TI-84 (5-1 p322 #69)
A Tangent Line Confirmed with the TI-84 (5-1 p322 #69)
Taking the Derivative of a Log Function (5-1 p322 #55)
Taking the Derivative of a Log Function (5-1 p322 #55)
We use the quotient rule together in this example.
U-substitution with a Definite Integral (4-R p310 #67)
U-substitution with a Definite Integral (4-R p310 #67)
When you use u-substitution with a definite integral, you don't have to switch back to make an expression in terms of x. Since any definite integral is the signed area, it is just a number. After finding the anti-derivative in terms of you, the FTC can be used to arrive at the answer.
Using the u-substitution Technique with an Indefinite Integral (4-R p301 #59)
Using the u-substitution Technique with an Indefinite Integral (4-R p301 #59)
A basic example of how to integrate something that looks like a product, where one factor has something in common with the derivative of the other factor.
Basic Use of the First Fundamental Theorem (4-R p 310 #41)
Basic Use of the First Fundamental Theorem (4-R p 310 #41)
Here we use the First Fundamental Theorem of Calculus to evaluate a definite integral, and we will check our work with a TI-84 calculator,
Riemann Sums to Estimate an Integral (4-R p 309 #25)
Riemann Sums to Estimate an Integral (4-R p 309 #25)
Here we use left and right Riemann sums to get the upeer and lower bounds on an integral. We can then use the TI-84 to check our work.
Sunday, January 10, 2021
Mean Value Theorem for Integrals with the TI-84 (4-5#85)
Mean Value Theorem for Integrals with the TI-84 (4-5#85)
Estimating Average Sales with t he TI-84 and the Mean Value Theorem for Integrals (4-5#85)
Summer Topic: Domains
Not all functions can take any number. The set of numbers that the function can accept is called a domain. Here we review how to analyze a ...

-
Not all functions can take any number. The set of numbers that the function can accept is called a domain. Here we review how to analyze a ...
-
How to use a TI-84 to find the volume of a hollow solid (which is ofter referred to "the washer" method since our circular cross...
-
Inverse Functions Have Reciprocal Slopes (5.R p 400 #39)